| Citation: Lu Zong-yue, Liu Gen-yuan, Zhao Xi-dong, Sun Kang, Chen Yan-si, Song Zhi-hong, Xue Kai, Yang Ming-shan. 2024. Landslide susceptibility assessment based on an interpretable coupled FR-RF model: A case study of Longyan City, Fujian province, Southeast China. China Geology. doi: 10.31035/cg2024123. |
Landslides emerge as one of the most common geologic hazards, causing numerous casualties and property losses every year (Ali R et al., 2020). Their disastrous consequences have impelled relevant researchers worldwide to actively develop methods for predicting the potential locations of landslides to mitigate these impacts (Peduto D et al., 2018; Meena SR et al., 2022). As a result, landslide susceptibility assessment models with high accuracy and reliability have attracted significant academic interest, aimed at predicting the spatial probability distribution of landslides to support the risk assessment and prevention of regional landslides (Chen Z and Song DQ, 2023; Huang FM et al., 2024).
Over the past few decades, numerous models for landslide susceptibility assessment have been developed, including the analytic hierarchy process (Regmi AD et al., 2014), the weight of evidence approach (Abraham MT et al., 2021), the information value and frequency ratio method, and machine learning models like logistic regression, support vector machines (SVMs), and RF (Wang HB et al., 2005). In recent years, machine learning models have become prominent due to their high accuracy compared to traditional heuristic and statistical models (Reichenbach P et al., 2018; Achour Y and Pourghasemi HR, 2020). These models can automatically analyze the contributions of various influencing factors (Youssef AM and Pourghasemi HR, 2021). However, their evaluation results often lack clarity, making it challenging to delineate the specific roles of different factors. While machine learning models can achieve high predictive accuracy without human intervention, statistical models excel at correlating with influencing factors. Therefore, combining machine learning and statistical models can help mitigate the limitations of both approaches and enhance overall prediction accuracy. Recently, coupled models that integrate multiple statistical methods or machine learning algorithms have been widely applied in landslide susceptibility assessments. Additionally, some researchers have explored coupled models, which combine multiple models and leverage their interdependencies to enhance assessment accuracy and generalizability (Zhao Z et al., 2021). Arabameri A et al. (2019) assessed the landslide sensitivity and risk of the Santalar Mountains watershed in Mazandaran Province, Iran, using statistical and artificial intelligence models like the FR-RF model, along with digital elevation models (DEMs) of different spatial resolutions. The results indicate that the FR-RF model exhibited high accuracy (0.917) in predicting landslide occurrence. He WC et al. (2023) analyzed the occurrence of landslides in Weixin County. Using models, researchers assessed the landslide risk while considering various environmental factors like terrain, geology, meteorology, and land cover. They found that coupled models (combining different methods) were more accurate than single models, especially the FR-RF model, which had an accuracy of up to 94.9%. These studies highlight the significant advantages of integrating the Frequency Ratio model with the Random Forest model into a coupled framework. The Frequency Ratio is a straightforward and effective statistical method that intuitively quantifies the relationship between various influencing factors and landslide occurrence. Its transparent and easily understandable calculation process makes it suitable for the preliminary selection of key factors, providing a solid statistical foundation for the model (Pandey VK et al., 2020). In contrast, Random Forest is a robust machine learning algorithm adept at handling high-dimensional data and capturing complex nonlinear relationships. By constructing multiple decision trees and aggregating their votes, it significantly enhances the model predictive power and stability. Moreover, Random Forest effectively manages missing values and noise, allowing the model to perform robustly under diverse environmental conditions. By combining the Frequency Ratio and Random Forest, this study can leverage the strengths of both: the Frequency Ratio provides valuable assessments of influencing factors, while Random Forest enhances predictive capabilities by learning complex data patterns. This complementarity not only improves the model predictive performance but also increases the credibility of the assessment results (Wang YL et al., 2024).
In addition, the accurate extraction of non-landslide points is an essential component in building a coupled model. The correct and reasonable selection of non-landslide points significantly impacts the accuracy and reliability of regional landslide susceptibility models (Huang FM et al., 2020). Optimizing the selection process for non-landslide points can also help mitigate the issue of model overfitting (Zhu AX et al., 2018). Currently, most researchers utilize a random selection method to extract non-landslide points (Pereira FF et al., 2023; Li MX et al., 2024). A major drawback of this approach is the risk of selecting non-landslide points from areas that may experience landslides in the future. For instance, Choi attempted to randomly select non-landslide points from areas with a slope of 0; however, the evaluation results indicated that the contribution of the slope factor was significantly greater than that of other factors (Choi J et al., 2012). Kavzoglu T et al. (2014) employed high-resolution Google Earth imagery to analyze low-slope areas, such as rivers and valleys, in the study area, selecting non-landslide points from these regions. While this method ensures the stability of non-landslide points, it may either exaggerate or downplay the contribution of the slope factor to the susceptibility model. Liu LL et al. (2022) initially evaluated the study area using the frequency ratio method and then randomly selected non-landslide points from areas categorized as extremely low and low susceptibility. Comparative results demonstrated a significant improvement in the accuracy of the refined model.
Despite the impressive performance of machine learning models in enhancing the accuracy of landslide susceptibility assessments, concerns regarding their “black-box” nature and model interpretability have emerged (Ozturk U et al., 2021). Some studies have addressed this issue by calculating the importance of influencing factor features using the Gini index (Sajadi P et al., 2022; Shahabi H et al., 2023). While this method helps identify key features that significantly impact model predictions, it does not quantify the specific influence of each feature on the target value or indicate whether the impact is positive or negative. The interpretability of a model is crucial to the decision-making process, contributing to the development of various interpretation algorithms such as partial dependence plot (PDP), individual conditional expectation (ICE), local interpretable model-agnostic explanations (LIME), and SHAP (Pradhan B et al., 2023). SHAP, introduced into the field of machine learning by Lundberg SM in 2020 (Lundberg SM et al., 2020), is an innovative interpretability model that employs the Shapley value principle from game theory to accurately evaluate the average contribution of each feature to model predictions. In landslide susceptibility assessment, SHAP effectively quantifies the importance of each influencing factor and their interdependencies, revealing the primary controlling factors and coupling mechanisms of regional landslides. This provides a fresh perspective for understanding the dynamics of landslide occurrence (Chen Z et al., 2023). The SHAP algorithm, known for its simplicity and broad applicability, quantifies the importance and contributions of factors both globally and locally, providing valuable interpretative insights for the application of machine learning models (Ekmekcioğlu Ö and Koc K, 2022; Zhou XZ et al., 2022; Zhang JY et al., 2023). However, the application of SHAP in landslide susceptibility research is still in its infancy. Strengthening the exploration of its uncertainties and enhancing its interpretability are important directions for current research.
In this study, the authors adopt a coupled model that integrates the Frequency Ratio and Random Forest models to simulate landslide occurrences in Longyan City. The authors also construct independent Random Forest models for comparison to verify the accuracy of the coupled model. The objectives of this study are twofold: (1) to develop a coupled model for assessing landslide susceptibility in Longyan City, and (2) to explore the interpretability of machine learning models. By analyzing 646 landslide points and nine influencing factors, the authors evaluate the model predictive performance using metrics such as precision, recall, F1 score, Kappa coefficient (KC), Overall Accuracy (OA), Brier score, Receiver Operating Characteristic (ROC) curve, and Precision-Recall (PR) curve. For the analysis of model interpretability, the authors employ the SHAP algorithm and Gini Index.
Longyan City, located in the hilly region comprising middle and low hills in western Fujian Province (Fig. 1), covers an area of approximately 19000 km2, with mountains and hills representing 78.6% of the total area. Under the influence of multi-stage tectonic activity and large-scale magma intrusion, this city exhibits complex geologic structures including well-developed folds and faults. It has a subtropical monsoon climate characterized by heavy and concentrated rainfall. Besides, it is characterized by a steep lithospheric slope and poor stability. All these establish the study area as a hotbed for geologic hazards.
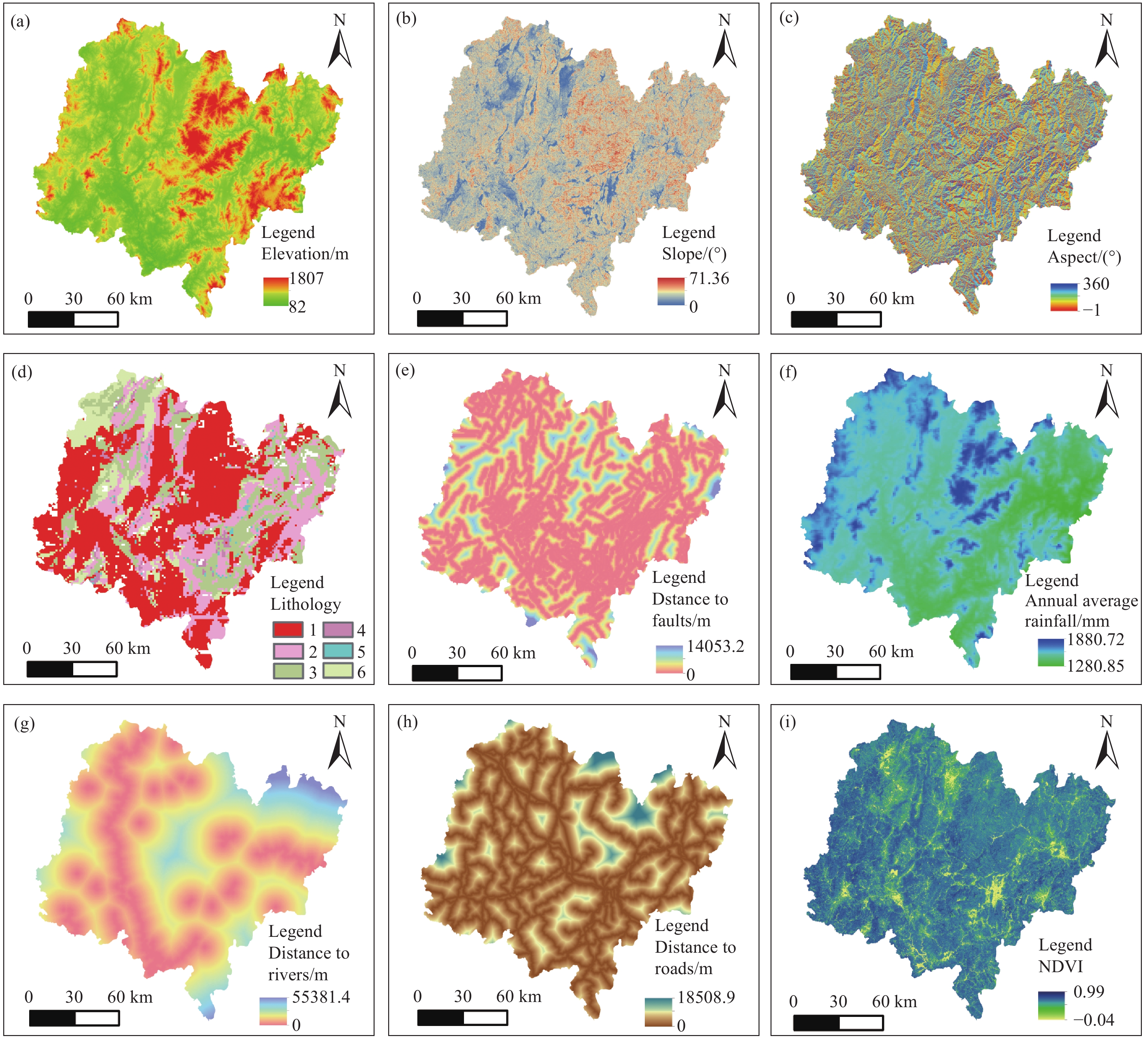
Factors suitable to use in landslide susceptibility assessment remain controversial. Based on previous studies (Huang FM et al., 2017; Zhou C et al., 2022) and the specific conditions of the study area, this study selected nine influential factors related to topography, geology, meteorology and hydrology, human activities, and vegetation cover (Table 1) : elevation, slope, aspect, lithology, distances from faults, rivers, and roads, average annual rainfall, and NDVI. Fig. 2 depicts nine thematic layers of influential factors, with a pixel size of 30×30 m. Among the nine influential factors, the rainfall was set at the average annual rainfall in Longyan City from 2013 to 2022. The impacts of various influential factors on landslide occurrence have been extensively explained previously (Achu A et al., 2023; Dai XL et al., 2023).
| Category | Evaluation factor | Source |
| Topography | Elevation | 30 m resolution DEM data for Longyan City from Geospatial Data Cloud (http://www.gscloud.cn) |
| Slope | ||
| Aspect | ||
| Geology | Lithology | National geological data Museum (https://www.ngac.cn/125cms/c/qggnew/index.htm) (Li CY et al., 1957; Li CY et al., 2019) |
| Distance from faults | ||
| Meteorology and hydrology |
Average annual rainfall | National Tibetan Plateau Data Center (https://data.tpdc.ac.cn/zh-hans/data/faae7605-a0f2-4d18-b28f-5cee413766a2) (Ding YX and Peng SZ, 2020; Peng SZ, 2020; Peng SZ et al., 2019; Peng SZ et al., 2017; Peng SZ et al., 2018) |
| Distance from rivers | National Platform for Common Geospatial Information Services (https://www.tianditu.gov.cn/) | |
| Human activities | Distance from roads | National Platform for Common Geospatial Information Services (https://www.tianditu.gov.cn/) |
| Vegetation | NDVI | National Ecosystem Science Data (http://www.nesdc.org.cn/sdo/detail?id=60f68d757e28174f0e7d8d49) (Dong JW et al., 2021; Yang JL et al., 2019) |
This study obtained the landslide inventory data from the Resource and Environment Science and Data Center of the Chinese Academy of Sciences (https://www.resdc.cn). These data have been validated and widely recognized for their reliability (Yao KZ et al., 2022; Yuan R and Chen J, 2022). A total of 646 landslides were recorded in the study area. Building on previous findings, this paper employs the frequency ratio model for the initial susceptibility assessment. Subsequently, 646 non-landslide points were randomly selected from areas classified as having extremely low and low susceptibility to serve as negative samples for the Random Forests Model.
The modeling process for landslide susceptibility assessment consisted of five steps (Fig. 3): (1) Influential factors were screened. Appropriate influential factors were selected based on previous studies and the specific conditions of the study area. Then, these factors were screened for assessment through the correlation analysis; (2) The sample dataset was established. Positive samples (landslide points) can be collected from field surveys, Google imagery, relevant departments, and related websites. Negative samples (non-landslide points) were selected using a FR model, rather than random generation, for an initial assessment of the study area. Then, based on the assessment results, non-landslide points, equal in numbers to the positive samples, were randomly selected from identified zones with very low and low susceptibility to form prediction samples. All samples were divided into a training set and a test set at a ratio of 7∶3; (3) The model was trained. The dataset composed of influential factors and positive/negative samples was put into the coupled FR-RF model for model training; (4) The coupled FR-RF model was assessed using various metrics; (5) The trained model was used to map landslide susceptibility in the study area and conduct statistical analysis.
For landslide susceptibility assessment using machine learning methods, it is necessary to ensure the independence of influential factors. Feature selection is a crucial step in machine learning, aimed at reducing the overfitting possibility and improving the generalization capability by eliminating redundant and less useful variables (Kumar C et al., 2023). The multicollinearity of influential factors it may lead to overfitting or underfitting problems (Dou J et al., 2015; Pham BT et al., 2018). The variance inflation factor (VIF) is a general index of multicollinearity, and the equation is as follows:
| VIF=11−R2 |
where R2 is the coefficient of determination, representing the degree of fitting of the model obtained using linear regression to a sample. 0<VIF<10, 10⩽VIF<100, and VIF⩾100 denote no, high, and severe multicollinearity, respectively.
Another criterion for testing the multicollinearity of influential factors is the tolerance (TOL), which is the reciprocal VIF value and can be calculated as follows:
| TOL=1VIF |
The TOL represents the amount of variation in the selected influential factor explained by other influential factors. TOL<0.1 and TOL>0.1 suggest the presence and absence of multicollinearity between factors, respectively.
A coupled model integrates the advantages of two or more models, thereby effectively enhancing the prediction accuracy (Yuan XY et al., 2022). To assess landslide susceptibility, this study used a coupled model combining the FR and the RF models.
The FR can be defined as the ratio of the percentage of disaster grid cells within a specific factor classification interval to the percentage of grid cells of the classification interval in the entire study area (Lee S and Pradhan B, 2007). It can be calculated as follows:
| FR=Fj/FCj/C |
where Fj is the number of disaster grid cells within a specific factor classification interval; F is the total number of disaster grid cells in the study area; Cj is the number of grid cells in the specific factor classification interval, and C indicates the total number of grid cells in the study area.
The RF, based on decision trees and bagging, is an ensemble learning algorithm proposed by Breiman L (2001). The RF model exhibits fewer errors under a larger sample size, many assessment factors, and a low possibility of overfitting (Li MX et al., 2024) and, thus, can effectively identify and capture the importance of variables. Furthermore, this model shows high tolerance to outliers and noise in the dataset. All these establish this model as the best machine learning model currently (Ghorbanzadeh O et al., 2019; Shahzad N et al., 2022). Compared to other machine learning models, the RF model enables more accurate landslide susceptibility assessment (Liu MY et al., 2023; Youssef AM et al., 2016). Besides, the RF model can avoid overfitting by controlling the number of decision trees (Catani F et al., 2013).
The specific workflow of the coupled FR-RF model is as follows: First, the sensitivity values of the influential factors were calculated using the FR model. These values were then used as classification data for the FR model. Besides, the FR model was also used as a prior model for an initial landslide susceptibility assessment. Based on the assessment results, 646 non-landslide points were randomly selected from zones with very low and low susceptibility levels. These non-landslide points served as negative samples for the FR model. Finally, 646 landslide points and 646 non-landslide points were divided into training and test data a ratio of 7∶3. The training data were used to build the landslide susceptibility assessment model, while the test data were utilized to validate the model’s prediction accuracy.
The confusion matrix provides a comprehensive and quantitative assessment of the performance of a classification model (Chen W et al., 2018). Based on the confusion matrix (Fig. 4), metrics such as precision, recall, F1-score, Kappa coefficient (KC), overall accuracy (OA), brier score, the Receiver Operating Characteristic (ROC) curve and the Precision-Recall (PR) curve can be calculated (Goetz J et al., 2015; Sun DL et al., 2021).
Precision is the proportion of true positive (TP) predictions among all samples predicted as positive:
| Precision=TPTP+FP |
Recall refers to the proportion of true positive (TP) predictions relative to all actual positive samples (TP + FN):
| Recall=TPTP+FN |
The F1 is defined as the harmonic mean of precision and recall, serving as a comprehensive assessment metric. It can be calculated as follows:
| F1=2×Precision×RecallPrecision+Recall |
The KC is a measure of consistency and classification performance. It is calculated based on the confusion matrix, ranging from −1 to 1 and typically above 0. A more unbalanced confusion matrix suggests a lower KC value, effectively penalizing models biased towards certain classes. It can be calculated as follows:
| Pe=(TP+FN)+(TP+FP)+(TN+FN)+(TN+FP)(TP+TN+FP+FN)2 |
| Kappa=Pp−Pe1−Pe |
OA is defined as the proportion of correct judgments among all judgments made, representing the accuracy of the model in classifying landslides and non-landslides. Specifically, it counts correct classifications as positive and incorrect classifications as negative:
| OA=TP+TNTP+TN+FP+FN |
The brier score is a metric used to assess the accuracy of probability predictions, particularly in binary classification problems. It measures model performance by calculating the mean squared difference between predicted probabilities and actual outcomes. The brier score ranges from 0 to 1, with values closer to 0 indicating higher predictive accuracy. Generally, a brier score below 0.25 is considered good, particularly in the context of imbalanced datasets.
ROC curves are extensively used to assess the overall performance of a model. The x-axis represents the false positive rate (FPR), which corresponds to specificity. FPR indicates the proportion of actual negative samples that are incorrectly classified as positive by the classifier. The y-axis represents the true positive rate (TPR), also known as sensitivity or recall. TPR indicates the proportion of actual positive samples that are correctly classified as positive by the classifier. The ROC curve can be plotted based on the confusion matrix, with x- and y-axes denoting FPR and TP, respectively. FPR and TPR can be calculated as follows:
| FPR=FPTN+FP |
| TPR=TPTP+FN |
FPR represents the ratio of negative samples incorrectly classified as positive to the total number of negative samples, while TPR (True Positive Rate) indicates the ratio of positive samples correctly predicted as positive to the total number of positive samples.
A ROC curve closer to the y-axis suggests higher predictive performance of the model. In landslide susceptibility assessment using the ROC curve, the area enclosed by the ROC curve and the x-axis (AUC) is typically used to measure the model's prediction accuracy. The AUC values range from 0 to 1, with values closer to 1 indicating higher model performance. Generally, AUC values above 0.8, between 0.7 and 0.8, and below 0.7 suggest good, fair, and poor model prediction, respectively. A value of 0.5 represents random guessing.
The Precision-Recall (PR) curve is another important tool for evaluating model performance. This curve plots Recall on the horizontal axis and Precision on the vertical axis. Recall measures the proportion of all positive samples correctly predicted by the model, while Precision reflects the proportion of truly positive samples among all samples predicted as positive. Ideally, the closer the PR curve is to the upper right corner, the better the model classification effectiveness, highlighting its ability to distinguish between positive and negative samples.
In this study, nine influential factors were selected for grading. Their FRs were calculated using the FR method (Table 2). Elevation was divided into five natural intervals. An increased elevation corresponded to gradually decreased FRs. The results reveal that 46% of landslides were concentrated at elevations ranging from 82 to 409 m. Slope was divided into six grades. Slopes ranging from 0˚ to 30˚ accounted for nearly 90% of landslides, whereas zones steeper than 50˚ experienced no landslides. Aspect exerted insignificant impacts on landslides since landslides occured in various directions. Concerning lithology, 46.7% of landslides occurred in intrusions, indicating that these rocks are more prone to landslides. Distance from faults was divided into seven levels, with 86.8% of landslides occurring within 3000 m of faults. A longer distance from faults was associated with a lower proportion of landslides, highlighting the significant impacts of distance from faults on landslide occurrence. Average annual rainfall was divided into five levels, and its increase resulted in gradually decreased FRs. Distances from rivers and roads were both divided into seven levels, with 42.3% of landslides occurring within 1000 m of roads. Table 2 shows that the proportion of landslides increased gradually with NDVI, indicating high landslide frequencies in zones with dense vegetation cover.
| Factor | Level | Radio of landslides | Ratio of domain | FR |
| Elevation (m) | 82–409 | 0.460 | 0.285 | 1.611 |
| 409–594 | 0.283 | 0.298 | 0.949 | |
| 594–804 | 0.167 | 0.225 | 0.743 | |
| 804–1076 | 0.080 | 0.137 | 0.588 | |
| 1076–1807 | 0.009 | 0.054 | 0.171 | |
| Slope (˚) | 0–10 | 0.300 | 0.206 | 1.458 |
| 10–20 | 0.402 | 0.386 | 1.044 | |
| 20–30 | 0.237 | 0.302 | 0.785 | |
| 30–40 | 0.053 | 0.092 | 0.572 | |
| 40–50 | 0.008 | 0.014 | 0.570 | |
| > 50 | 0.000 | 0.001 | 0.000 | |
| Aspect (˚) | Plane (−1) | 0.005 | 0.005 | 1.022 |
| North (0–22.5&337.5–360) | 0.116 | 0.120 | 0.970 | |
| Northeast (22.5–67.5) | 0.125 | 0.114 | 1.102 | |
| East (67.5–112.5) | 0.128 | 0.129 | 0.995 | |
| Southeast (112.5–157.5) | 0.149 | 0.132 | 1.129 | |
| South (157.5–202.5) | 0.169 | 0.126 | 1.344 | |
| Southwest (202.5–247.5) | 0.118 | 0.125 | 0.939 | |
| West (247.5–292.5) | 0.108 | 0.129 | 0.839 | |
| Northwest (292.5–337.5) | 0.082 | 0121 | 0.678 | |
| Lithology | intrusive rock | 0.467 | 0.473 | 0.988 |
| Sandstone and siltstone | 0.229 | 0.231 | 0.994 | |
| Strata containing mudstone, shale, and coal | 0.189 | 0.188 | 1.005 | |
| Loose sediments | 0.031 | 0.013 | 2.302 | |
| Carbonate rock | 0.010 | 0.006 | 1.580 | |
| Metamorphic rock | 0.075 | 0.090 | 0.835 | |
| Distance from faults (m) | 0–1000 | 0.451 | 0.471 | 0.957 |
| 1000–2000 | 0.225 | 0.235 | 0.956 | |
| 2000–3000 | 0.192 | 0.163 | 1.177 | |
| 3000–4000 | 0.064 | 0.063 | 1.005 | |
| 4000–5000 | 0.034 | 0.037 | 0.922 | |
| 5000–6000 | 0.023 | 0.022 | 1.081 | |
| > 6000 | 0.011 | 0.008 | 1.305 | |
| Annual average rainfall (mm) | 1280–1447 | 0.259 | 0.162 | 1.597 |
| 1447–1520 | 0.276 | 0.217 | 1.270 | |
| 1520–1589 | 0.286 | 0.315 | 0.910 | |
| 1589–1673 | 0.152 | 0.227 | 0.667 | |
| 1673–1881 | 0.028 | 0.079 | 0.353 | |
| Distance from rivers (m) | 0–1000 | 0.060 | 0.045 | 1.334 |
| 1000–2000 | 0.036 | 0.048 | 0.747 | |
| 2000–3000 | 0.045 | 0.045 | 1.008 | |
| 3000–4000 | 0.034 | 0.034 | 1.008 | |
| 4000–5000 | 0.073 | 0.061 | 1.194 | |
| 5000–6000 | 0.050 | 0.053 | 0.930 | |
| > 6000 | 0.703 | 0.715 | 0.984 | |
| Distance from roads (m) | 0–1000 | 0.423 | 0.276 | 1.529 |
| 1000–2000 | 0.119 | 0.191 | 0.624 | |
| 2000–3000 | 0.116 | 0.148 | 0.784 | |
| 3000–4000 | 0.111 | 0.114 | 0.978 | |
| 4000–5000 | 0.051 | 0.086 | 0.595 | |
| 5000–6000 | 0.056 | 0.061 | 0.910 | |
| > 6000 | 0.124 | 0.123 | 1.004 | |
| NDVI | 0–0.45 | 0.033 | 0.020 | 1.602 |
| 0.45–0.67 | 0.119 | 0.036 | 3.322 | |
| 0.67–0.80 | 0.224 | 0.094 | 2.380 | |
| 0.80–0.87 | 0.407 | 0.397 | 1.024 | |
| 0.87–1.00 | 0.217 | 0.452 | 0.479 |
In this study, multicollinearity was employed to analyze the dependence of influential factors on each other. The analytical results indicate that the VIF values ranged from 1.68 to 1.02 and the TOL values varied from 0.98 to 0.60 (Table 3). Given that VIF<10 and TOL>0.1 indicated the absence of multicollinearity, all the nine influential factors proved independent and thus can be used for landslide susceptibility assessment.
| Influencing factor | VIF | TOL |
| Elevation | 1.68 | 0.60 |
| Slope | 1.22 | 0.82 |
| Aspect | 1.02 | 0.98 |
| Lithology | 1.06 | 0.94 |
| Distance from faults | 1.03 | 0.97 |
| Annual average rainfall | 1.51 | 0.66 |
| Distance from rivers | 1.06 | 0.94 |
| Distance from roads | 1.08 | 0.92 |
| NDVI | 1.21 | 0.82 |
To verify the advantages of the coupled model, this study selected a single Random Forest model for comparison. The accuracy evaluation results in Table 4 show that the various indicators of the coupled model significantly outperform those of the single random forest model. According to the confusion matrix, the coupled model achieves a precision of 0.89, a recall of 0.88, an F1-score of 0.88, a kappa coefficient of 0.77, an overall accuracy of 0.88, and a brier score of 0.11 (Table 4). These favorable evaluation results indicate that the coupled model performs well in probability prediction.
| Evaluation metric | Precision | Recall | F1-score | Kappa coefficient | Overall accuracy | Brier score |
| RF | 0.82 | 0.82 | 0.82 | 0.64 | 0.82 | 0.18 |
| FR-RF | 0.89 | 0.88 | 0.88 | 0.77 | 0.88 | 0.11 |
Similarly, the ROC and PR curves presented in Fig. 5 demonstrate the higher accuracy of the coupled model. Fig. 5 (a) displays the ROC curve, which is close to the upper left corner and exhibits a smooth shape, indicating that the model maintains a high true positive rate across various thresholds while keeping the false positive rate low. This suggests that the model is effective at distinguishing between positive and negative instances when identifying landslide events, with an area under the curve is 0.93, reflecting its strong predictive capability for landslide susceptibility. The PR curve in Fig. 5 (b) is very close to the upper right corner, indicating that the model maintains high precision alongside a high recall rate, with an area under the curve is 0.95, further demonstrating its effectiveness. This performance can serve as a valuable reference for risk management strategies.
This study conducted a probabilistic forecast of landslide susceptibility across the study area using the coupled FR-RF model, creating a susceptibility assessment map. Based on geometric interval classification, the study area was categorized into five susceptibility levels: very low, low, moderate, high, and very high (Fig. 6).
The study area, with 646 landslides, was divided into 25842893 grid cells (Table 5). Zones with very low susceptibility covered 22% of the total area and eight landslides (1%). Zones with low susceptibility manifested an area proportion of 26% and 91 landslides (14%). Zones with moderate susceptibility displayed an area proportion of 14% and 106 landslides (16%). Zones with high susceptibility displayed an area proportion of 14% and a landslide percentage of 18% (115). Zones with very high susceptibility covered 24% of the total area and 326 landslides (51%). Zones with very high and high susceptibility exhibited a total area proportion of 38% and 69% of landslides. A higher landslide susceptibility level corresponded to a higher landslide proportion, indicating a significant positive correlation between both. Therefore, the assessment results align highly with the actual conditions.
| Landslide susceptibility | Grid number | Cell proportion (%) | Landslides number | Proportion (%) |
| Very low | 5659699 | 22 | 8 | 1 |
| Low | 6692799 | 26 | 91 | 14 |
| Moderate | 3708865 | 14 | 106 | 16 |
| High | 3521133 | 14 | 115 | 18 |
| Very high | 6260397 | 24 | 326 | 51 |
| Total | 25842893 | 100 | 646 | 100 |
Limited interpretability restricts the application of machine learning models to landslide susceptibility assessment (Zhou XZ et al., 2022), posing a significant threat to relevant projects. Therefore, this study conducted model interpretation using the SHAP algorithm and the Gini index.
A honeycomb plot (Fig. 7) is a method that combines the magnitude and weights of feature values to visualize the impacts of individual factors on assessment results (Wang D et al., 2022). In this plot, each cell represents a SHAP value of a feature. Labels show the names of features sorted by importance. Each point in the honeycomb plot represents a real sample. The colors of points are determined by feature values, with red colors indicating high values. The size of the central concave cross-section denotes the number of points with the same SHAP value, corresponding to the magnitude of features. The positions of feature values suggest the contributions of various features to the assessment results. A value closer to the right side of the plot facilitates the outcome, while a value closer to the left inhibits it. Fig. 7 shows that distance from roads, NDVI, elevation, and rainfall produced significant impacts on landslide occurrence.
SHAP values are more reliable compared to traditional measures of feature importance (Al-Najjar HA et al., 2023). They represent the numerical values of various influential factors in the model, indicating the importance of influential factors. Fig. 8 illustrates the SHAP values of the RF model, with the influential factors arranged in descending order of importance. The SHAP results indicate that distance from roads, NDVI, and elevation had the most significant impacts on landslides, followed by rainfall, slope, aspect, distance from faults and rivers, and lithology sequentially.
The feature importance analysis based on the RF classifier provided deeper insights into the key determinants of landslide susceptibility in the study area. The feature importance was assessed using the Gini index. Specifically, the Gini index of each feature was compared with the average Gini index of all features. If the Gini index of a feature exceeds the average, the feature has high importance; conversely, a lower Gini index corresponds to lower importance. Among the features, distance from roads proved to be the most significant influential factor in landslide prediction, followed by elevation. In contrast, the relatively low importance of distance from rivers indicates a weak impact on landslide susceptibility (Fig. 9).
Currently, the application of machine learning to landslide susceptibility assessment has been recognized by scientists worldwide (Shahabi H and Hashim M, 2015). However, debates persist about the machine learning model with high assessment precision (Ma ZJ et al., 2021). Precision can be calculated and assessed based on various factors, leading to a significant increase in the number of high-precision assessment models (Cascini L et al., 2015; Lombardo L et al., 2020).
This study conducted a landslide susceptibility assessment in the research area using a coupled model that combines frequency ratio and random forest techniques. The model performance was evaluated using metrics such as the Receiver Operating Characteristic (ROC) and Precision-Recall (PR) curves, resulting in Area Under the Curve (AUC) values of 0.93 and 0.95, indicating high precision in evaluation. The primary advantages of the coupled FR-RF model are as follows: (1) The FR model was employed to conduct an initial landslide susceptibility assessment, generating random points in zones with very low and low landslide susceptibility as negative samples for the RF model. This approach ensured the diversity of negative samples and significantly reduced the likelihood that negative samples fell into potential landslide zones, thereby maximizing the correct selection of negative samples; (2) The FR values of various influential factors were used as the input of the RF model, contributing to enhanced accuracy and predictive capability of landslide susceptibility assessment. Traditional machine learning methods tend to neglect the impacts of event frequency on assessment results, whereas this approach comprehensively captured the variations in the probability of landslides by integrating FRs.
The novelty of this study lies in its introduction of the concept of interpretability. Model interpretability aids researchers in gaining a deeper understanding of the model reasoning process and plays a crucial role in its generalization ability (Linardatos P et al., 2020). Specifically, interpretability clarifies how the model makes predictions or decisions, thereby enhancing trust and comprehension. This understanding helps identify the model limitations or errors in specific situations, facilitating improvements in model design and application. Furthermore, interpretability highlights key factors influencing model performance and enables better adaptation to new data or different environments, enhancing its generalization capability. Thus, by improving model interpretability, the predictive ability and applicability of the model can be effectively enhanced across various scenarios.
While the random forest model can rank the importance of influencing factors using the Gini index, it cannot specifically indicate each factor contribution to individual landslide events. In contrast, the SHAP algorithm presents the model overall trends and specific situations from both global and local perspectives, facilitating a better understanding of the model behavior within the dataset (Qiu HJ et al., 2024). In this study, the authors interpreted the model using both the SHAP algorithm and Gini index calculation methods. The results indicate that the importance rankings of influencing factors are generally similar between the two methods, with distance to roads consistently ranking first. However, factors with similar impact levels exhibit slight differences in ranking, stemming from the fundamental differences in their principles. The SHAP algorithm evaluates each feature contribution to predictions, computing the impact of each feature value on those predictions. Consequently, SHAP values accurately measure each feature influence on model predictions, considering both intrinsic importance and the effect of feature values (Lundberg SM et al., 2020). In contrast, the Gini index assesses a feature contribution to decision tree node splits, focusing on how features affect the construction and predictive capabilities of the model decision trees. The SHAP algorithm provides a more detailed and comprehensive assessment of feature importance by accounting for the specific impact of feature values on predictions, beyond just the features themselves. This is particularly valuable for understanding how features influence predictions under varying conditions and for interpreting model predictions in decision-making. Thus, if deeper insights into how each feature value affects individual prediction instances are needed, SHAP serves as a more explanatory tool. Conversely, random forest feature importance is more suitable for large-scale datasets and scenarios requiring efficient computation of feature importance (Wang HJ et al., 2024).
Through the SHAP algorithm and random forest feature importance analysis, this study consistently identifies distance from roads as the predominant factor influencing landslides in Longyan City. Zeng TR et al. (2023) considered that landslide susceptibility is dynamic, particularly in the context of rapid urban and road network expansion. This dynamic characteristic is especially evident in the coastal regions in eastern China, where extensive engineering activities significantly affect the occurrence of landslides (Dong N et al., 2018). Zeng TR et al. (2023) investigated the impacts of road networks on landslide susceptibility, finding that the density of landslides gradually decreases with increasing distance from roads. A survey of different road networks from 2016 to 2020 reveals that an increase in the number of roads led to significantly increased zones with high landslide susceptibility. Kulsoom I et al. (2023) conducted a landslide susceptibility assessment of the Karakoram Highway, revealing the significant impacts of roads on landslides. Rohan T et al. (2023) found that urbanized areas in the southern Pennsylvania region tend to be more susceptible to landslides, indicating a strong correlation between landslides and the distance from roads. The interpretable model developed in this study suggests that human activities play a crucial role in landslides in the area. Road construction introduces new factors, such as excavation, tunneling, and filling, which compromise slope stability. Furthermore, once roads are completed, vibrations from vehicles may lead to slope deformation, potentially triggering landslides. Therefore, in our study area, road expansion is identified as the primary driving factor for landslides. Consequently, it is recommended that local governments prioritize slope protection measures during road construction to mitigate the risk of future landslides.
SHAP is an effective algorithm for interpreting landslide susceptibility assessment results, capable of measuring the relative importance and interactions of various influencing factors. This capability enables researchers to gain a comprehensive understanding of the distribution characteristics of each factor during the modeling process, as well as the patterns of landslide occurrences. Consequently, it enhances the credibility of machine learning algorithms and provides valuable insights for interpretability research. I believe SHAP will play an indispensable role in the future of machine learning studies. However, this study has some limitations. For instance, in addition to the two types of visualizations used in this paper, the SHAP algorithm also encompasses various other visual methods, such as scatter plots and heatmaps. Future research could further explore the significance of these visualizations in enhancing models explanations, thereby establishing more reliable interpretable models. Moreover, this paper introduces SHAP as one algorithm for model interpretation; future studies could investigate other algorithms for broaden the scope of model explanation.
The spatial heterogeneity of influential factors like geological environments can result in varying predictive capacities of a model across different study areas. Kulsoom I et al. (2023) assessed the landslide susceptibility of the Karakoram Highway using five models: extreme gradient boosting (XGBoost), RF, artificial neural network (ANN), Naïve Bayes (NB), and K-nearest neighbors (KNN). They compared the accuracy of these models using the ROC curve, obtaining AUC values of 99.74, 99.36, 98.82, 98.46, and 92.43, respectively, suggesting that the XGBoost model has the highest accuracy. Similarly, Yao JM et al. (2023) investigated the upper reaches of the Jinsha River using four machine learning models, obtaining AUC values of 90.767 (RF), 90.24 (XGBoost), 86.939 (logistic regression), and 80.136 (SVM), suggesting the RF's superior assessment accuracy. Therefore, regarding the model generalization capability, applying RF or deep learning techniques in landslide susceptibility assessment requires further in-depth research (Chen YS et al., 2021). Consequently, it proves challenging to develop a model with a high generalization capability that consistently maintains optimal performance across various study areas (Zeng TR et al., 2023).
In recent years, deep learning techniques have demonstrated remarkable effectiveness in assessing landslide susceptibility (Ullah K et al., 2022; Prakash N et al., 2020; Dou J et al., 2020). By efficiently extracting multidimensional feature information and capturing complex nonlinear relationships, these methods have significantly improved the accuracy of landslide predictions. Notably, Convolutional Neural Networks (CNNs) and Long Short-Term Memory networks (LSTMs) excel in autonomously learning critical features from large datasets, minimizing reliance on manual feature selection, and adeptly processing unstructured data. As a result, deep learning is emerging as an indispensable tool for enhancing landslide prediction accuracy and bolstering disaster risk reduction, particularly in complex geological settings where it surpasses traditional approaches. The ongoing advancement and refinement of deep learning techniques hold great promise for developing more precise and reliable tools for landslide susceptibility assessment, thereby driving progress in disaster prevention and mitigation technologies.
Coupled models present promising avenues for achieving more robust predictions. This study explores the integration of traditional and machine-learning models. Future research could delve into the coupling of different machine learning techniques. Moreover, coupled models based on deep learning warrant more research efforts to enhance the accuracy and precision of landslide susceptibility assessment.
In this study, nine influential factors related to topography, geology, meteorology and hydrology, human activities, and vegetation cover were extracted from multiple data sources. An initial landslide susceptibility assessment of the study area was conducted using a FR model. Based on the assessment results, non-landslide points were randomly selected from zones with very low and low landslide susceptibility as negative samples. Then, the landslide susceptibility in the study area was assessed using the coupled FR-RF model. Finally, the model's explanatory power was analyzed using the SHAP algorithm and the Gini index. Key findings from this study are as follows:
(i) The evaluation metrics of the coupled model are significantly higher than those of the random forest model, demonstrating excellent classification ability. The landslide susceptibility map reveals that 69% of the landslides are distributed in zones with very high and high landslide susceptibility, indicating the high consistency of the map.
(ii) Based on the assessment results of the coupled FR-RF model, the study area can be divided into five susceptibility levels: very low, low, moderate, high, and very high. A higher susceptibility level corresponds to a higher likelihood of landslides, aligning with the actual conditions. This provides crucial spatial information for the early warning and response efforts of geologic hazards.
(iii) SHAP values effectively reflect the mechanisms behind the landslide susceptibility assessment of the coupled FR-RF model. Dominant factors influencing landslide susceptibility in the study area include distance from roads, NDVI, and elevation. It is recommended that local governments prioritize slope protection measures during road construction to prevent potential landslides.
(iv) Despite some results achieved, this study encountered some challenges. Subsequent research could integrate more new technologies and finer-scale spatial data to enhance the predictive and generalization capabilities of models.
Zong-yue Lu, Gen-yuan Liu, Xi-dong Zhao, Yan-si Chen and Kang Sun conceived of the presented idea. Zong-yue Lu, Yan-si Chen and Kang Sun carried out the experiment. All authors discussed the results and contributed to the final manuscript.
The authors declare no conflicts of interest.
This research was supported by the project of the China Geological Survey (DD20230591). The datasets of rainfall are provided by National Tibetan Plateau / Third Pole Environment Data Center (http://data.tpdc.ac.cn). The Normalized Difference Vegetation Index dataset is provided by National Ecosystem Science Data Center, National Science & Technology Infrastructure of China. (http://www.nesdc.org.cn).
|
Abraham MT, Satyam N, Lokesh R, Pradhan B, Alamri A. 2021. Factors affecting landslide susceptibility mapping: Assessing the influence of different machine learning approaches, sampling strategies and data splitting. Land, 10(9), 989. doi: 10.3390/land10090989.
|
|
Achour Y, Pourghasemi HR. 2020. How do machine learning techniques help in increasing accuracy of landslide susceptibility maps? Geoscience Frontiers, 11(3), 871–883. doi: 10.1016/j.gsf.2019.10.001.
|
|
Achu AL, Aju CD, Di Napoli M, Prakash P, Gopinath G, Shaji E, Chandra V. 2023. Machine-learning based landslide susceptibility modelling with emphasis on uncertainty analysis. Geoscience Frontiers, 14(6), 101657. doi: 10.1016/j.gsf.2023.101657.
|
|
Al-Najjar HAH, Pradhan B, Beydoun G, Sarkar R, Park HJ, Alamri A. 2023. A novel method using explainable artificial intelligence (XAI)-based Shapley Additive Explanations for spatial landslide prediction using Time-Series SAR dataset. Gondwana Research, 123, 107–124. doi: 10.1016/j.gr.2022.08.004.
|
|
Ali R, Kuriqi A, Kisi O. 2020. Human–environment natural disasters interconnection in China: A review. Climate, 8(4), 48. doi: 10.3390/cli8040048.
|
|
Arabameri A, Pradhan B, Rezaei K, Lee CW. 2019. Assessment of landslide susceptibility using statistical- and artificial intelligence-based FR–RF integrated model and multiresolution DEMs. Remote Sensing, 11(9), 999. doi: 10.3390/rs11090999.
|
|
Breiman L. 2001. Random forests. Machine Learning, 45(1), 5–32. doi: 10.1023/A: 1010933404324. doi: 10.1023/A:1010933404324.
|
|
Cascini L, Ciurleo M, Di Nocera S, Gullà G. 2015. A new–old approach for shallow landslide analysis and susceptibility zoning in fine-grained weathered soils of southern Italy. Geomorphology, 241, 371–381. doi: 10.1016/j.geomorph.2015.04.017.[LinkOut.
|
|
Catani F, Lagomarsino D, Segoni S, Tofani V. 2013. Landslide susceptibility estimation by random forests technique: Sensitivity and scaling issues. Natural Hazards and Earth System Sciences, 13(11), 2815–2831. doi: 10.5194/nhess-13-2815-2013.
|
|
Chen W, Zhang S, Li R, Shahabi H. 2018. Performance evaluation of the GIS-based data mining techniques of best-first decision tree, random forest, and naïve Bayes tree for landslide susceptibility modeling. Science of the Total Environment, 644, 1006–1018. doi: 10.1016/j.scitotenv.2018.06.389.
|
|
Chen YS, Hou JL, Huang CH, Zhang Y, Li XH. 2021. Mapping maize area in heterogeneous agricultural landscape with multi-temporal sentinel-1 and sentinel-2 images based on random forest. Remote Sensing, 13(15), 2988. doi: 10.3390/rs13152988.
|
|
Chen Z, Chang RC, Pei XJ, Yu ZB, Guo HD, He ZQ, Zhao WB, Zhang QP, Chen Y. 2023. Tunnel geothermal disaster susceptibility evaluation based on interpretable ensemble learning: A case study in Ya’an–Changdu section of the Sichuan–Tibet traffic corridor. Engineering Geology, 313, 106985. doi: 10.1016/j.enggeo.2023.106985.
|
|
Chen Z, Song DQ. 2023. Modeling landslide susceptibility based on convolutional neural network coupling with metaheuristic optimization algorithms. International Journal of Digital Earth, 16(1), 3384–3416. doi: 10.1080/17538947.2023.2249863.
|
|
Choi J, Oh HJ, Lee HJ, Lee C, Lee S. 2012. Combining landslide susceptibility maps obtained from frequency ratio, logistic regression, and artificial neural network models using ASTER images and GIS. Engineering Geology, 124, 12–23. doi: 10.1016/j.enggeo.2011.09.011.
|
|
Dai XL, Zhu YQ, Sun K, Zou Q, Zhao S, Li WR, Hu L, Wang S. 2023. Examining the spatially varying relationships between landslide susceptibility and conditioning factors using a geographical random forest approach: A case study in Liangshan, China. Remote Sensing, 15(6), 1513. doi: 10.3390/rs15061513.
|
|
Ding YX, Peng SZ. 2020. Spatiotemporal trends and attribution of drought across China from 1901–2100. Sustainability, 12(2), 477. doi: 10.3390/su12020477.
|
|
Dong JW, Zhou Y, You NS. 2021. China 30m Annual Maximum NDVI Dataset from 2000 to 2022 [DS/OL]. National Ecosystem Science Data Center. doi: https://doi.org/10.12199/nesdc.ecodb.rs.2021.012.
|
|
Dong N, You L, Cai WJ, Li G, Lin H. 2018. Land use projections in China under global socioeconomic and emission scenarios: Utilizing a scenario-based land-use change assessment framework. Global Environmental Change, 50, 164–177. doi: 10.1016/j.gloenvcha.2018.04.001.
|
|
Dou J, Yamagishi H, Pourghasemi HR, Yunus AP, Song X, Xu YR, Zhu ZF. 2015. An integrated artificial neural network model for the landslide susceptibility assessment of Osado Island, Japan. Natural Hazards, 78(3), 1749–1776. doi: 10.1007/s11069-015-1799-2.
|
|
Dou J, Yunus AP, Merghadi A, Shirzadi A, Nguyen H, Hussain Y, Avtar R, Chen YL, Pham BT, Yamagishi H. 2020. Different sampling strategies for predicting landslide susceptibilities are deemed less consequential with deep learning. Science of The Total Environment, 720, 137320. doi: 10.1016/j.scitotenv.2020.137320.
|
|
Ekmekcioğlu Ö, Koc K. 2022. Explainable step-wise binary classification for the susceptibility assessment of geo-hydrological hazards. Catena, 216, 106379. doi: 10.1016/j.catena.2022.106379.
|
|
Ghorbanzadeh O, Blaschke T, Gholamnia K, Meena SR, Tiede D, Aryal J. 2019. Evaluation of different machine learning methods and deep-learning convolutional neural networks for landslide detection. Remote Sensing, 11(2), 196. doi: 10.3390/rs11020196.
|
|
Goetz JN, Brenning A, Petschko H, Leopold P. 2015. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Computers & Geosciences, 81, 1–11. doi: 10.1016/j.cageo.2015.04.007.
|
|
He WC, Chen GP, Zhao JS, Lin YL, Qin BG, Yao WL, Cao Q. 2023. Landslide susceptibility evaluation of machine learning based on information volume and frequency ratio: A case study of Weixin County, China. Sensors, 23(5), 2549. doi: 10.3390/s23052549.
|
|
Huang FM, Cao ZS, Jiang SH, Zhou CB, Huang JS, Guo ZZ. 2020. Landslide susceptibility prediction based on a semi-supervised multiple-layer perceptron model. Landslides, 17(12), 2919–2930. doi: 10.1007/s10346-020-01473-9.
|
|
Huang FM, Teng ZK, Yao C, Jiang SH, Catani F, Chen W, Huang JS. 2024. Uncertainties of landslide susceptibility prediction: Influences of random errors in landslide conditioning factors and errors reduction by low pass filter method. Journal of Rock Mechanics and Geotechnical Engineering, 16(1), 213–230. doi: 10.1016/j.jrmge.2023.11.001.
|
|
Huang FM, Yin KL, Huang JS, Gui L, Wang P. 2017. Landslide susceptibility mapping based on self-organizing-map network and extreme learning machine. Engineering Geology, 223, 11–22. doi: 10.1016/j.enggeo.2017.04.013.
|
|
Kavzoglu T, Sahin EK, Colkesen I. 2014. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides, 11(3), 425–439. doi: 10.1007/s10346-013-0391-7.
|
|
Kulsoom I, Hua WH, Hussain S, Chen QH, Khan G, Dai SH. 2023. SBAS-InSAR based validated landslide susceptibility mapping along the karakoram highway: A case study of Gilgit-Baltistan, Pakistan. Scientific Reports, 13, 3344. doi: 10.1038/s41598-023-30009-z.
|
|
Kumar C, Walton G, Santi P, Luza C. 2023. An ensemble approach of feature selection and machine learning models for regional landslide susceptibility mapping in the arid mountainous terrain of southern Peru. Remote Sensing, 15(5), 1376. doi: 10.3390/rs15051376.
|
|
Lee S, Pradhan B. 2007. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides, 4(1), 33–41. doi: 10.1007/s10346-006-0047-y.
|
|
Li CY, Wang XC, He CZ, Wu X, Kong ZY, Li XL. 1957. China national digital geological map (public version at 1∶200000 scale) spatial database (V1) [DB]. Development and Research Center, China Geological Survey, China Geological Survey, National Geological Archives of China. doi: 10.12029/gc2019Z101.
|
|
Li CY, Wang XC, He CZ, Wu X, Kong ZY, Li XL. 2019. China national digital geological map (public version at 1∶200000 scale) spatial database. Geology in China, 46(S1), 1–10. doi: 10.12029/gc2019Z101.
|
|
Li MX, Wang HY, Chen JL, Zheng K. 2024. Assessing landslide susceptibility based on the random forest model and multi-source heterogeneous data. Ecological Indicators, 158, 111600. doi: 10.1016/j.ecolind.2024.111600.
|
|
Linardatos P, Papastefanopoulos V, Kotsiantis S. 2020. Explainable AI: A review of machine learning interpretability methods. Entropy, 23(1), 18. doi: 10.3390/e23010018.
|
|
Liu LL, Zhang YL, Xiao T, Yang C. 2022. A frequency ratio–based sampling strategy for landslide susceptibility assessment. Bulletin of Engineering Geology and the Environment, 81(9), 360. doi: 10.1007/s10064-022-02836-3.
|
|
Liu MY, Xu B, Li ZW, Mao WX, Zhu Y, Hou JX, Liu WZ. 2023. Landslide susceptibility zoning in Yunnan Province based on SBAS-InSAR technology and a random forest model. Remote Sensing, 15(11), 2864. doi: 10.3390/rs15112864.
|
|
Lombardo L, Opitz T, Ardizzone F, Guzzetti F, Huser R. 2020. Space-time landslide predictive modelling. Earth-Science Reviews, 209, 103318. doi: 10.1016/j.earscirev.2020.103318.
|
|
Lundberg SM, Erion G, Chen H, DeGrave A, Prutkin JM, Nair B, Katz R, Himmelfarb J, Bansal N, Lee SI. 2020. From local explanations to global understanding with explainable AI for trees. Nature Machine Intelligence, 2(1), 56–67. doi: 10.1038/s42256-019-0138-9.
|
|
Ma ZJ, Mei G, Piccialli F. 2021. Machine learning for landslides prevention: A survey. Neural Computing and Applications, 33(17), 10881–10907. doi: 10.1007/s00521-020-05529-8.
|
|
Meena SR, Soares LP, Grohmann CH, Van Westen C, Bhuyan K, Singh RP, Floris M, Catani F. 2022. Landslide detection in the Himalayas using machine learning algorithms and U-Net. Landslides, 19(5), 1209–1229. doi: 10.1007/s10346-022-01861-3.
|
|
Ozturk U, Pittore M, Behling R, Roessner S, Andreani L, Korup O. 2021. How robust are landslide susceptibility estimates? Landslides, 18(2), 681–695. doi: 10.1007/s10346-020-01485-5.
|
|
Pandey VK, Pourghasemi HR, Sharma MC. 2020. Landslide susceptibility mapping using maximum entropy and support vector machine models along the highway corridor, Garhwal Himalaya. Geocarto International, 35(2), 168–187. doi: 10.1080/10106049.2018.1510038.
|
|
Peduto D, Nicodemo G, Caraffa M, Gullà G. 2018. Quantitative analysis of consequences to masonry buildings interacting with slow-moving landslide mechanisms: A case study. Landslides, 15(10), 2017–2030. doi: 10.1007/s10346-018-1014-0.
|
|
Peng SZ. (2020). 1-km monthly precipitation dataset for China (1901‒2022): National Tibetan Plateau Data Center. doi: https://doi.org/10.5281/zenodo.3114194.
|
|
Peng SZ, Ding YX, Liu WZ, Li Z. 2019. 1 km monthly temperature and precipitation dataset for China from 1901 to 2017. Earth System Science Data, 11(4), 1931–1946. doi: 10.5194/essd-11-1931-2019.
|
|
Peng SZ, Ding YX, Wen ZM, Chen YM, Cao Y, Ren JY. 2017. Spatiotemporal change and trend analysis of potential evapotranspiration over the Loess Plateau of China during 2011–2100. Agricultural and Forest Meteorology, 233, 183–194. doi: 10.1016/j.agrformet.2016.11.129.
|
|
Peng SZ, Gang CC, Cao Y, Chen YM. 2018. Assessment of climate change trends over the Loess Plateau in China from 1901 to 2100. International Journal of Climatology, 38(5), 2250–2264. doi: 10.1002/joc.5331.
|
|
França Pereira F, Sussel Gonçalves Mendes T, Jorge Coelho Simões S, Roberto Magalhães de Andrade M, Luiz Lopes Reiss M, Fortes Cavalcante Renk J, Correia da Silva Santos T. 2023. Comparison of LiDAR- and UAV-derived data for landslide susceptibility mapping using Random Forest algorithm. Landslides, 20(3), 579–600. doi: 10.1007/s10346-022-02001-7.
|
|
Pham BT, Prakash I, Singh SK, Shirzadi A, Shahabi H, Tran TTT, Bui DT. 2019. Landslide susceptibility modeling using reduced error pruning trees and different ensemble techniques: Hybrid machine learning approaches. Catena, 175, 203–218. doi: 10.1016/j.catena.2018.12.018.
|
|
Pradhan B, Dikshit A, Lee S, Kim H. 2023. An explainable AI (XAI) model for landslide susceptibility modeling. Applied Soft Computing, 142, 110324. doi: 10.1016/j.asoc.2023.110324.
|
|
Prakash N, Manconi A, Loew S. 2020. Mapping landslides on EO data: Performance of deep learning models vs. traditional machine learning models. Remote Sensing, 12(3), 346. doi: 10.3390/rs12030346.
|
|
Qiu HJ, Xu Y, Tang BZ, Su LL, Li YJ, Yang DD, Ullah M. 2024. Interpretable landslide susceptibility evaluation based on model optimization. Land, 13(5), 639. doi: 10.3390/land13050639.
|
|
Regmi AD, Devkota KC, Yoshida K, Pradhan B, Pourghasemi HR, Kumamoto T, Akgun A. 2014. Application of frequency ratio, statistical index, and weights-of-evidence models and their comparison in landslide susceptibility mapping in Central Nepal Himalaya. Arabian Journal of Geosciences, 7(2), 725–742. doi: 10.1007/s12517-012-0807-z.
|
|
Reichenbach P, Rossi M, Malamud BD, Mihir M, Guzzetti F. 2018. A review of statistically-based landslide susceptibility models. Earth-Science Reviews, 180, 60–91. doi: 10.1016/j.earscirev.2018.03.001.
|
|
Rohan T, Shelef E, Mirus B, Coleman T. 2023. Prolonged influence of urbanization on landslide susceptibility. Landslides, 20(7), 1433–1447. doi: 10.1007/s10346-023-02050-6.
|
|
Sajadi P, Sang YF, Gholamnia M, Bonafoni S, Mukherjee S. 2022. Evaluation of the landslide susceptibility and its spatial difference in the whole Qinghai-Tibetan Plateau region by five learning algorithms. Geoscience Letters, 9(1), 9. doi: 10.1186/s40562-022-00218-x.
|
|
Shahabi H, Ahmadi R, Alizadeh M, Hashim M, Al-Ansari N, Shirzadi A, Wolf ID, Ariffin EH. 2023. Landslide susceptibility mapping in a mountainous area using machine learning algorithms. Remote Sensing, 15(12), 3112. doi: 10.3390/rs15123112.
|
|
Shahabi H, Hashim M. 2015. Landslide susceptibility mapping using GIS-based statistical models and Remote sensing data in tropical environment. Scientific Reports, 5, 9899. doi: 10.1038/srep09899.
|
|
Shahzad N, Ding X, Abbas S. 2022. A comparative assessment of machine learning models for landslide susceptibility mapping in the rugged terrain of northern Pakistan. Applied Sciences, 12(5), 2280. doi: 10.3390/app12052280.
|
|
Sun DL, Xu JH, Wen HJ, Wang DZ. 2021. Assessment of landslide susceptibility mapping based on Bayesian hyperparameter optimization: A comparison between logistic regression and random forest. Engineering Geology, 281, 105972. doi: 10.1016/j.enggeo.2020.105972.
|
|
Ullah K, Wang Y, Fang ZC, Wang LZ, Rahman M. 2022. Multi-hazard susceptibility mapping based on Convolutional Neural Networks. Geoscience Frontiers, 13(5), 101425. doi: 10.1016/j.gsf.2022.101425.
|
|
Wang D, Thunéll S, Lindberg U, Jiang L, Trygg J, Tysklind M. 2022. Towards better process management in wastewater treatment plants: Process analytics based on SHAP values for tree-based machine learning methods. Journal of Environmental Management, 301, 113941. doi: 10.1016/j.jenvman.2021.113941.
|
|
Wang HB, Liu GJ, Xu WY, Wang GH. 2005. GIS-based landslide hazard assessment: An overview. Progress in Physical Geography: Earth and Environment, 29(4), 548–567. doi: 10.1191/0309133305pp462ra.
|
|
Wang HJ, Liang QX, Hancock JT, Khoshgoftaar TM. 2024. Feature selection strategies: A comparative analysis of SHAP-value and importance-based methods. Journal of Big Data, 11(1), 44. doi: 10.1186/s40537-024-00905-w.
|
|
Wang YL, Ling YB, Chan TO, Awange J. 2024. High-resolution earthquake-induced landslide hazard assessment in Southwest China through frequency ratio analysis and LightGBM. International Journal of Applied Earth Observation and Geoinformation, 131, 103947. doi: 10.1016/j.jag.2024.103947.
|
|
Yang JL, Dong JW, Xiao XM, Dai JH, Wu CY, Xia JY, Zhao GS, Zhao MM, Li ZL, Zhang Y, Ge Q. 2019. Divergent shifts in peak photosynthesis timing of temperate and alpine grasslands in China. Remote Sensing of Environment, 233, 111395. doi: 10.1016/j.rse.2019.111395.
|
|
Yao JM, Yao X, Zhao Z, Liu XH. 2023. Performance comparison of landslide susceptibility mapping under multiple machine-learning based models considering InSAR deformation: A case study of the upper Jinsha River. Geomatics, Natural Hazards and Risk, 14(1), 2212833. doi: 10.1080/19475705.2023.2212833.
|
|
Yao KZ, Yang SN, Wu SN, Tong B. 2022. Landslide susceptibility assessment considering spatial agglomeration and dispersion characteristics: A case study of Bijie City in Guizhou Province, China. ISPRS International Journal of Geo-Information, 11(5), 269. doi: 10.3390/ijgi11050269.
|
|
Youssef AM, Pourghasemi HR. 2021. Landslide susceptibility mapping using machine learning algorithms and comparison of their performance at Abha Basin, Asir Region, Saudi Arabia. Geoscience Frontiers, 12(2), 639–655. doi: 10.1016/j.gsf.2020.05.010.
|
|
Youssef AM, Pourghasemi HR, Pourtaghi ZS, Al-Katheeri MM. 2016. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides, 13(5), 839–856. doi: 10.1007/s10346-015-0614-1.
|
|
Yuan R, Chen J. 2022. A hybrid deep learning method for landslide susceptibility analysis with the application of InSAR data. Natural Hazards, 114(2), 1393–1426. doi: 10.1007/s11069-022-05430-8.
|
|
Yuan XY, Liu C, Nie RH, Yang ZL, Li WL, Dai XA, Cheng JY, Zhang JM, Ma L, Fu X, Tang M, Xu YN, Lu H. 2022. A comparative analysis of certainty factor-based machine learning methods for collapse and landslide susceptibility mapping in Wenchuan County, China. Remote Sensing, 14(14), 3259. doi: 10.3390/rs14143259.
|
|
Zeng TR, Wu LY, Peduto D, Glade T, Hayakawa YS, Yin KL. 2023. Ensemble learning framework for landslide susceptibility mapping: Different basic classifier and ensemble strategy. Geoscience Frontiers, 14(6), 101645. doi: 10.1016/j.gsf.2023.101645.
|
|
Zhang JY, Ma XL, Zhang JL, Sun DL, Zhou XZ, Mi CL, Wen HJ. 2023. Insights into geospatial heterogeneity of landslide susceptibility based on the SHAP-XGBoost model. Journal of Environmental Management, 332, 117357. doi: 10.1016/j.jenvman.2023.117357.
|
|
Zhao Z, Liu ZY, Xu C. 2021. Slope unit-based landslide susceptibility mapping using certainty factor, support vector machine, random forest, CF-SVM and CF-RF models. Frontiers in Earth Science, 9, 589630. doi: 10.3389/feart.2021.589630.
|
|
Zhou C, Cao Y, Hu X, Yin KL, Wang Y, Catani F. 2022. Enhanced dynamic landslide hazard mapping using MT-InSAR method in the Three Gorges Reservoir Area. Landslides, 19(7), 1585–1597. doi: 10.1007/s10346-021-01796-1.
|
|
Zhou XZ, Wen HJ, Li ZW, Zhang H, Zhang WG. 2022. An interpretable model for the susceptibility of rainfall-induced shallow landslides based on SHAP and XGBoost. Geocarto International, 37(26), 13419–13450. doi: 10.1080/10106049.2022.2076928.
|
|
Zhu AX, Miao YM, Yang L, Bai SB, Liu JZ, Hong HY. 2018. Comparison of the presence-only method and presence-absence method in landslide susceptibility mapping. Catena, 171, 222–233. doi: 10.1016/j.catena.2018.07.012.
|
| Category | Evaluation factor | Source |
| Topography | Elevation | 30 m resolution DEM data for Longyan City from Geospatial Data Cloud (http://www.gscloud.cn) |
| Slope | ||
| Aspect | ||
| Geology | Lithology | National geological data Museum (https://www.ngac.cn/125cms/c/qggnew/index.htm) (Li CY et al., 1957; Li CY et al., 2019) |
| Distance from faults | ||
| Meteorology and hydrology |
Average annual rainfall | National Tibetan Plateau Data Center (https://data.tpdc.ac.cn/zh-hans/data/faae7605-a0f2-4d18-b28f-5cee413766a2) (Ding YX and Peng SZ, 2020; Peng SZ, 2020; Peng SZ et al., 2019; Peng SZ et al., 2017; Peng SZ et al., 2018) |
| Distance from rivers | National Platform for Common Geospatial Information Services (https://www.tianditu.gov.cn/) | |
| Human activities | Distance from roads | National Platform for Common Geospatial Information Services (https://www.tianditu.gov.cn/) |
| Vegetation | NDVI | National Ecosystem Science Data (http://www.nesdc.org.cn/sdo/detail?id=60f68d757e28174f0e7d8d49) (Dong JW et al., 2021; Yang JL et al., 2019) |
| Factor | Level | Radio of landslides | Ratio of domain | FR |
| Elevation (m) | 82–409 | 0.460 | 0.285 | 1.611 |
| 409–594 | 0.283 | 0.298 | 0.949 | |
| 594–804 | 0.167 | 0.225 | 0.743 | |
| 804–1076 | 0.080 | 0.137 | 0.588 | |
| 1076–1807 | 0.009 | 0.054 | 0.171 | |
| Slope (˚) | 0–10 | 0.300 | 0.206 | 1.458 |
| 10–20 | 0.402 | 0.386 | 1.044 | |
| 20–30 | 0.237 | 0.302 | 0.785 | |
| 30–40 | 0.053 | 0.092 | 0.572 | |
| 40–50 | 0.008 | 0.014 | 0.570 | |
| > 50 | 0.000 | 0.001 | 0.000 | |
| Aspect (˚) | Plane (−1) | 0.005 | 0.005 | 1.022 |
| North (0–22.5&337.5–360) | 0.116 | 0.120 | 0.970 | |
| Northeast (22.5–67.5) | 0.125 | 0.114 | 1.102 | |
| East (67.5–112.5) | 0.128 | 0.129 | 0.995 | |
| Southeast (112.5–157.5) | 0.149 | 0.132 | 1.129 | |
| South (157.5–202.5) | 0.169 | 0.126 | 1.344 | |
| Southwest (202.5–247.5) | 0.118 | 0.125 | 0.939 | |
| West (247.5–292.5) | 0.108 | 0.129 | 0.839 | |
| Northwest (292.5–337.5) | 0.082 | 0121 | 0.678 | |
| Lithology | intrusive rock | 0.467 | 0.473 | 0.988 |
| Sandstone and siltstone | 0.229 | 0.231 | 0.994 | |
| Strata containing mudstone, shale, and coal | 0.189 | 0.188 | 1.005 | |
| Loose sediments | 0.031 | 0.013 | 2.302 | |
| Carbonate rock | 0.010 | 0.006 | 1.580 | |
| Metamorphic rock | 0.075 | 0.090 | 0.835 | |
| Distance from faults (m) | 0–1000 | 0.451 | 0.471 | 0.957 |
| 1000–2000 | 0.225 | 0.235 | 0.956 | |
| 2000–3000 | 0.192 | 0.163 | 1.177 | |
| 3000–4000 | 0.064 | 0.063 | 1.005 | |
| 4000–5000 | 0.034 | 0.037 | 0.922 | |
| 5000–6000 | 0.023 | 0.022 | 1.081 | |
| > 6000 | 0.011 | 0.008 | 1.305 | |
| Annual average rainfall (mm) | 1280–1447 | 0.259 | 0.162 | 1.597 |
| 1447–1520 | 0.276 | 0.217 | 1.270 | |
| 1520–1589 | 0.286 | 0.315 | 0.910 | |
| 1589–1673 | 0.152 | 0.227 | 0.667 | |
| 1673–1881 | 0.028 | 0.079 | 0.353 | |
| Distance from rivers (m) | 0–1000 | 0.060 | 0.045 | 1.334 |
| 1000–2000 | 0.036 | 0.048 | 0.747 | |
| 2000–3000 | 0.045 | 0.045 | 1.008 | |
| 3000–4000 | 0.034 | 0.034 | 1.008 | |
| 4000–5000 | 0.073 | 0.061 | 1.194 | |
| 5000–6000 | 0.050 | 0.053 | 0.930 | |
| > 6000 | 0.703 | 0.715 | 0.984 | |
| Distance from roads (m) | 0–1000 | 0.423 | 0.276 | 1.529 |
| 1000–2000 | 0.119 | 0.191 | 0.624 | |
| 2000–3000 | 0.116 | 0.148 | 0.784 | |
| 3000–4000 | 0.111 | 0.114 | 0.978 | |
| 4000–5000 | 0.051 | 0.086 | 0.595 | |
| 5000–6000 | 0.056 | 0.061 | 0.910 | |
| > 6000 | 0.124 | 0.123 | 1.004 | |
| NDVI | 0–0.45 | 0.033 | 0.020 | 1.602 |
| 0.45–0.67 | 0.119 | 0.036 | 3.322 | |
| 0.67–0.80 | 0.224 | 0.094 | 2.380 | |
| 0.80–0.87 | 0.407 | 0.397 | 1.024 | |
| 0.87–1.00 | 0.217 | 0.452 | 0.479 |
| Influencing factor | VIF | TOL |
| Elevation | 1.68 | 0.60 |
| Slope | 1.22 | 0.82 |
| Aspect | 1.02 | 0.98 |
| Lithology | 1.06 | 0.94 |
| Distance from faults | 1.03 | 0.97 |
| Annual average rainfall | 1.51 | 0.66 |
| Distance from rivers | 1.06 | 0.94 |
| Distance from roads | 1.08 | 0.92 |
| NDVI | 1.21 | 0.82 |
| Evaluation metric | Precision | Recall | F1-score | Kappa coefficient | Overall accuracy | Brier score |
| RF | 0.82 | 0.82 | 0.82 | 0.64 | 0.82 | 0.18 |
| FR-RF | 0.89 | 0.88 | 0.88 | 0.77 | 0.88 | 0.11 |
| Landslide susceptibility | Grid number | Cell proportion (%) | Landslides number | Proportion (%) |
| Very low | 5659699 | 22 | 8 | 1 |
| Low | 6692799 | 26 | 91 | 14 |
| Moderate | 3708865 | 14 | 106 | 16 |
| High | 3521133 | 14 | 115 | 18 |
| Very high | 6260397 | 24 | 326 | 51 |
| Total | 25842893 | 100 | 646 | 100 |